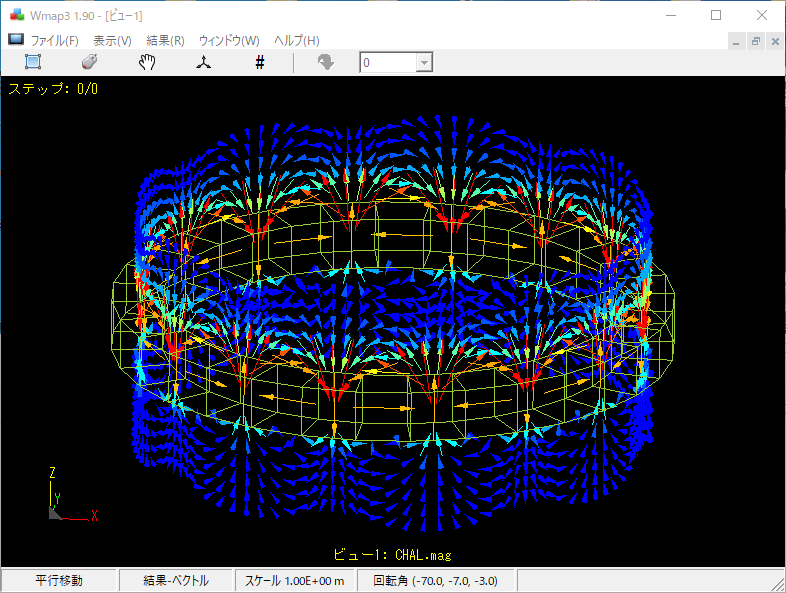
電磁界解析/電磁場解析ソフトウェア「ELF/MAGIC」
ELF シリーズではクーロンの法則やビオ・サバールの法則を使って、導体や磁性体の相互作用を連立方程式を立てて解きます。この解析手法は高速で精度よく計算可能である半面、メッシュの切り方によっては不安定な解が発生する場合がありました。
株式会社エルフは、この原因を解明し、メッシュの切り方によらず安定した解を得る解析手法を確立しました。
電磁界解析/電磁場解析ソフトウェア「ELF/MAGIC」推奨モデル
「ELF/MAGIC」推奨モデル
Microsoft® Windows® 10 Pro 64bit
インテル® Core™ i7-12700 プロセッサー
64GB(32GB x2) DDR4-3200 | Unbuffered | Non-ECC
500GB M.2 NVMe-SSD PCI Express 3.0(x4)
NVIDIA® T400 2GB-GDDR6 PCI Express 3.0(x16)
販売価格 239,800 円(税込)
※ 本製品には「ELF/MAGIC」は含まれておりません。「ELF/MAGIC」の価格については、営業担当までお問い合わせください。

お問い合わせ、ご相談は
こちらの専用窓口まで
西日本:06-6838-4123
東日本:03-5280-9255
ELF/MAGIC 電磁界解析/電磁場解析
- 空間メッシュはいりません(空間磁場は高精度)
有限要素法はポテンシャルを変数としています。したがって磁石やコイルなどの物体だけでなく、解析対象の空間全域に要素が必要です。
一方、ELF/MAGICは磁荷などのソースを変数としています。したがってソースが存在している物体のみの要素で解析できます。空間にはソースがないので要素は不要です。
メートルスケールの部品とマイクロメートルスケールの部品が混在するような解析モデルでも空間要素が不要なため、容易に解析できます。 - 境界条件はいりません
ELF/MAGICでは解析領域は無限遠までを含んでいます。
したがって境界条件を指定する必要がありません。 - 解析式による磁場の計算
ELF/MAGICでは要素の積分は複数の点での数値積分ではなく、要素表面の解析式を使っています。
したがって面の近くまで精度の高い計算ができます。 - 空間磁場が高精度
有限要素法では空間磁場の計算は、空間メッシュのポテンシャルから計算するので精度が落ちますが、ELF/MAGICでは磁場をソースから直接計算するので精度が落ちません。
ソースが作る磁場の計算は解析積分式を用いています。したがって磁場は要素近傍まで高精度です。
高精度の空間磁場を使って高精度の力、トルク、荷電粒子軌道解析などができます。MRI,磁気シールド、スパッタリング、センサ、ブラウン管などが精度良く解析できます。
- 空間メッシュはいりません(空間磁場は高精度)
- 粗い要素分割でも高精度
磁場は物体の外部で急激に小さくなっていきます。そのためポテンシャルは物体の外部で複雑な変化をします。
有限要素法で使用するポテンシャルは、物体外部で大きく変化します。したがって空間部は物体内部よりも細かな要素分割が必要です。さらに、3次元の磁場は3方向に広がるので2次元の磁場よりも急激に変化しますから、3次元解析は2次元解析よりも細かな要素分割が必要です。
一方、ELF/MAGICで使用するソースは、物体の内部や表面にのみ存在し、物体の外部には存在しません。たとえポテンシャルが複雑に変化する場所であっても、そこにソースが存在しなければ要素そのものが不要です。
また、要素を必要とする物体内や表面でのソースの変化は緩やかです。したがってELF/MAGICでは一般に有限要素法ほど細かな要素分割を必要としません。 - 3次元計算が高速
有限要素法は2次元計算は高速ですが、3次元計算は時間がかかります。
その理由は
・2次元ではポテンシャルは1自由度ですが3次元では3自由度です。
・空間部も含めて要素数が奥行き方向に増えます。
・マトリックスのバンド幅が増えます。
・2次元解析より細かい要素分割が必要です。
ELF/MAGICでは変数は増えますが、もともと少ない要素で解けます。
・基本的な3次元要素の自由度は2次元要素の1.5倍です。
・奥行き方向の要素の分割数は普通はあまり多くありません。 - 運動の取り扱いが容易
ELF/MAGICでは空間メッシュが必要ありません。
したがって、部品の相互の位置が変化しても、空間メッシュがねじれたりつぶれたりすることがありません。 - 複雑な形状のコイルが容易
ELF/MAGICでは空間メッシュが必要ありません。
したがって、任意の形状のコイルと電流方向を自由に指定することができます。
コイル内の磁場の変化を考える必要が無いので細かなメッシュにする必要がありません。
- 粗い要素分割でも高精度
解析の種類
- 静磁場解析
時間的に変化をしない磁場を解析します。 渦電流や誘導電流は計算しません。 磁性体のB-H曲線(非線形)が扱えます。 - 過渡応答解析
電流が変化する場合や物体が運動する場合の計算をします。 渦電流や誘導電流を計算します。 磁性体のB-H曲線(非線形)が扱えます。 空間メッシュがないため自由な運動が扱えます。
- 静磁場解析
- 周波数応答解析
周波数応答解析をします。 渦電流や誘導電流を計算します。 入力電流、磁化、渦電流が正弦波状に変化する場合を複素数を使って計算します。 複素透磁率を入力して短時間でインダクタンスの計算をすることもできます。
- 周波数応答解析
モデルの種類
- 3次元モデル
3次元形状の物体の磁場解析をします。 3次元形状のソースが作る磁場の解析積分式を使って計算します。 ELF/MAGICの基本的な解析です。 - 2次元モデル
Z方向に無限に長い形状の物体の磁場解析をします。 XY平面に物体の断面を定義することにより、 Z方向に無限に長いソースが作る磁場の解析積分式を使って計算します。
- 3次元モデル
- 軸対称モデル
円柱、円筒など、軸対称形状の物体で軸対称磁場の場合に利用できます。 XZ平面に物体の断面を定義することにより、 軸対称形状のソースを配置して解析します。
- 軸対称モデル
磁場解析事例 ELF/MAGIC
以下の計算時間はCore i7 6700K のPCでの計算時間 (秒)です。
- ハルバッハ配列磁石(直線状)
計算時間:1秒

磁石をハルバッハ配列(直線状)に並べて空間磁場を計算した事例です。磁石の片側だけに強い磁場が得られます。
- ハルバッハ配列磁石(直線状)
- ハルバッハ配列磁石(リング状)
計算時間:1秒

- ハルバッハ配列磁石(リング状)

お問い合わせ、ご相談は
こちらの専用窓口まで
西日本:06-6838-4123
東日本:03-5280-9255
HPC 製品 導入実績一覧
※敬称略、順不同
| 琉球大学 | 国立沖縄工業高等専門学校 | 名桜大学 | 沖縄科学技術大学院大学 | 沖縄国際大学 |
| 宮崎大学 | 宮崎公立大学 | 鹿児島大学 | 第一工業大学 | 鹿児島県立短期大学 |
| 鹿児島工業高等専門学校 | 鹿児島国際大学 | 鹿屋体育大学 | 長崎大学 | 国立佐世保工業高等専門学校 |
| 長崎県立大学 | 大分大学 | 日本文理大学 | 大分県立科学大学 | 大分工業高等専門学校 |
| 大分県立芸術文化短期大学 | 熊本大学 | 熊本県立大学 | 国立八代工業高等専門学校 | 国立熊本工業高等専門学校 |
| 九州看護福祉大学 | 九州大学 | 佐賀大学 | 福岡教育大学 | 福岡女子大学 |
| 佐賀大学 | 国立久留米工業高等専門学校 | 福岡県立大学 | 福岡大学 | 福岡工業大学 |
| 久留米工業大学 | 久留米大学 | 福岡歯科大学 | 九州産業大学 | 近畿大学(福岡キャンパス) |
| 国立有明工業高等専門学校 | 日本経済大学 | 九州工業大学 | 北九州市立大学 | 産業医科大学 |
| 九州歯科大学 | 国立北九州工業高等専門学校 | 西日本工業大学 | 早稲田大学(北九州キャンパス) | 山口大学 |
| 山口東京理科大学 | 山口県立大学 | 国立大島商船高等専門学校 | 国立宇部工業高等専門学校 | 島根大学 |
| 国立松江工業高等専門学校 | 鳥取大学 | 広島大学 | 県立広島大学 | 広島工業大学 |
| 広島市立大学 | 近畿大学(広島キャンパス) | 呉高専 | 広島修道大学 | 尾道市立大学 |
| 広島文化学園大学 | 岡山大学 | 岡山理科大学 | 倉敷芸術科学大学 | 岡山県立大学 |
| 川崎医療大学 | ノートルダム清心女子大学 | 岡山商科大学 | 吉備国際大学 | 川崎医療福祉大学 |
| 就実大学 | 愛媛大学 | 愛媛県立医療技術大学 | 岡山理科大学(今治キャンパス) | 国立新居浜工業高等専門学校 |
| 国立弓削商船高等専門学校 | 香川大学 | 国立香川工業高等専門学校 | 徳島大学 | 阿南工業高等専門学校 |
| 鳴門教育大学 | 高知大学 | 高知工科大学 | 国立高知工業高等専門学校 | 高知県立大学 |
| 神戸大学 | 兵庫教育大学 | 兵庫県立大学 | 関西学院大学 | 甲南大学 |
| 神戸学院大学 | 国立明石工業高等専門学校 | 大阪大学 | 大阪教育大学 | 大阪市立大学 |
| 大阪府立大学 | 大阪工業大学 | 大阪産業大学 | 大阪電気通信大学 | 関西大学 |
| 近畿大学(本学) | 大阪国際大学 | 摂南大学 | 大阪薬科大学 | 大阪医科大学 |
| 追手門学院大学 | 藍野大学 | 大阪人間科学大学 | 奈良女子大学 | 奈良先端科学技術大学院大学 |
| 奈良教育大学 | 奈良県立医科大学 | 国立奈良工業高等専門学校 | 和歌山大学 | 国立和歌山工業高等専門学校 |
| 京都大学 | 京都工芸繊維大学 | 京都教育大学 | 京都府立医科大学 | 京都府立大学 |
| 京都産業大学 | 立命館大学 | 京都先端科学大学 | 京都女子大学 | 京都橘大学 |
| 京都薬科大学 | 同志社大学 | 佛教大学 | 龍谷大学 | 京都市立芸術大学 |
| 国立舞鶴工業高等専門学校 | 滋賀大学 | 滋賀県立大学 | 滋賀医科大学 | 三重大学 |
| 国立鈴鹿工業高等専門学校 | 名古屋大学 | 名古屋工業大学 | 豊橋技術科学大学 | 愛知県立大学 |
| 愛知工業大学 | 中京大学 | 豊田工業大学 | 南山大学 | 中部大学 |
| 愛知教育大学 | 名古屋市立大学 | 愛知医科大学 | 愛知学院大学 | 大同学園 |
| 静岡大学 | 浜松医科大学 | 静岡県立大学 | 静岡文化芸術大学 | 国立遺伝学研究所 |
| 静岡理工科大学 | 岐阜大学 | 自然科学研究機構 | 核融合科学研究所 | 国立岐阜工業高等専門学校 |
| 岐阜薬科大学 | 朝日大学 | 信州大学 | 国立長野工業高等専門学校 | 山梨大学 |
| 山梨学院大学 | 都留文科大学 | 福井大学 | 金沢大学 | 石川県立大学 |
| 北陸先端科学技術大学院大学 | 北陸大学 | 金沢工業大学 | 富山大学 | 富山県立大学 |
| 新潟大学 | 長岡技術科学大学 | 上越教育大学 | 新潟県立看護大学 | 国立長岡工業高等専門学校 |
| 横浜国立大学 | 防衛大学校 | 横浜市立大学 | 北里大学 | 神奈川大学 |
| 関東学院大学 | 神奈川県立保健福祉大学 | 東京大学 | 東京医科歯科大学 | 東京海洋大学 |
| 一橋大学 | 電気通信大学 | 東京工業大学 | 北里大学 | 東京農工大学 |
| 東京都立大学 | 青山学院大学 | 國學院大學 | 駒沢大学 | 順天堂大学 |
| 専修大学 | 帝京大学 | 東京未来大学 | 東京理科大学 | 日本大学 |
| 明治大学 | 明星大学 | 学習院大学 | 慶応義塾大学 | 上智大学 |
| 創価大学 | 大東文化大学 | 中央大学 | 東海大学 | 東京医科大学 |
| 法政大学 | 立教大学 | 早稲田大学 | お茶の水女子大学 | 国立情報学研究所 |
| 東京学芸大学 | 東京外国語大学 | 国立東京工業専門学校 | 桜美林大学 | 工学院大学 |
| 関東学院大学 | 国際基督教大学 | 成蹊大学 | 芝浦工業大学 | 成城大学 |
| 昭和薬科大学 | 東京電機大学 | 東洋大学 | 獨協医科大学 | 拓殖大学 |
| 東京工科大学 | 津田塾大学 | 帝京平成大学 | 獨協大学 | 千葉大学 |
| 千葉工業大学 | 国立木更津工業高等専門学校 | 埼玉大学 | 防衛医科大学校 | 跡見学園女子大学 |
| 埼玉工業大学 | ものつくり大学 | 群馬大学 | 国立群馬工業高等専門学校 | 宇都宮大学 |
| 自治医科大学 | 国立小山工業高等専門学校 | 筑波大学 | 茨城大学 | 筑波技術大学 |
| 茨城工業高等専門学校 | 高エネルギー加速器研究機構 | 物質材料研究機構 | 国立環境研究所 | 建築研究所 |
| 理化学研究所 | 土木研究所 | 産業技術総合研究所 | 会津大学 | 福島県立医科大学 |
| 国立福島工業高等専門学校 | 山形大学 | 秋田大学 | 秋田県立大学 | 東北大学 |
| 宮城大学 | 宮城教育大学 | 東北工業大学 | 岩手大学 | 岩手県立大学 |
| 一関工業高等専門学校 | 岩手医科大学 | 弘前大学 | 国立八戸工業高等専門学校 | 北海道大学 |
| 公立はこだて未来大学 | 小樽商科大学 | 帯広畜産大学 | 北見工業大学 | 国立釧路工業高等専門学校 |
| 札幌医科大学 | 国立苫小牧工業高等専門学校 | 国立函館工業高等専門学校 |